Eureka!
As soon as you hear the name Archimedes, the first thing that comes to mind is either mathematics or science.
A well-known researcher and scientist, Archimedes proposed various laws and theories in the fields of motion, geometry, liquid motion, and more.

“Eureka!” was the word he shouted when he made a new discovery, some of which are listed below:
1. Archimedes’ Principle
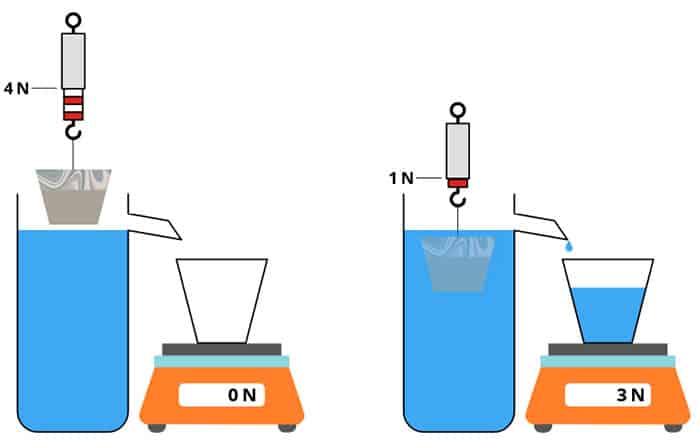
Archimedes principle is quite a challenging concept for many of us to grasp, but it basically concerns the theory of buoyancy.
When a solid body falls into a liquid, it displaces the same amount of liquid as the volume of the body immersed in it. A variety of forces act on a body in any liquid. Archimedes’ principle also helps us to understand why something floats or sinks by showing that the amount of liquid displaced is the measure of the sinking or rising capability of the object. The weight of the displaced liquid tells us if the object will float or sink.
This law has been instrumental in understanding maritime principles used by ships and submarines, all of which are designed using the buoyancy principle. The lactometer (an instrument used to measure the purity of milk) is also based on the above principle.
2. The Sand Reckoner
Imagine counting grains of sand! This is what Archimedes set out to do. The Sand Reckoner is a work by Archimedes in which he attempts to count the number of grains of sand it would take to cover the universe.
First, Archimedes had to work out how to count a number with a large base, leading him to take a major step in the field of mathematics. Until that time, the Greeks had represented the number system using various symbols. Archimedes established a new theory in mathematics which could count numbers to an infinite value.
The highest number ever counted is 8*1063, as demonstrated in Archimedes’ Sand Reckoner, where he estimated that it would take 8 *1063 grains of sand to cover the universe.
3. Evaluation of Pi (π)

Archimedes used the Hellenistic method of mathematics. Pi is a Greek symbol which is used in various formulae, and Archimedes was able to derive the value of Pi using his exceptional intellect.
Pi’s numerical value is approximately 3.14 which is calculated by dividing 22 by 7. Pi the ratio of the circumference of a circle to the diameter. Archimedes also circumscribed various shapes in the circle. Various applications of Pi have been seen in mathematics, such as working out the area of a circle. Pi can also be used to calculate the area of a sphere as well as of a hemisphere.
4. The Claw of Archimedes
Archimedes was from the coastal city of Syracuse in present-day Italy, then a Greek territory. To protect the city from enemies, Archimedes designed a hook that could latch on to an enemy ship and sink it. This was known as the Claw of Archimedes or “the iron hand.”
Archimedes was an architect as well as a scientist, and the Claw of Archimedes was also a magnificent piece of architecture which allowed the people of Syracuse to defend themselves against Roman invasion by sea. A warship could easily be overturned by the claw as Archimedes had taken into account the buoyancy of the water.
5. Archimedes’ Screw

Archimedes’ screw was more of a pump than a screw. It was used to pump water against gravity. The screw could be turned using any physical means such as manually or by wind using a windmill, and it was essential in helping farmers to irrigate their lands.
Carrying water from a low level to a higher level was a tough job, but Archimedes’ screw allowed this to be done easily by working against gravity. The Archimedes screw is still used today in various forms, such as plastic reforming machines, die casting machines, or injection molding machines. The fast rotating screws that help to pump water can also be used to generate electricity.
Developed countries around the world still use this technology for irrigation and to generate electricity through rotating turbines. The United States has developed a reverse screw hydropower plant, and the screw can also be used at times of flooding in low-lying areas.
6. Archimedes’ Death Ray
There is no doubt that Archimedes was a great inventor, and the death ray is no exception. This parabolic mirrored structure was used to concentrate sunlight over a particular area on a ship which would then catch fire, ultimately leading to the sinking of the ship.
The concept was again developed as a defensive mechanism for his city of Syracuse. By catching fire to enemy ships, they were able to defeat the faceless Roman army.
Some scientists consider this to be ineffective as the ships are in constant motion, but a few years ago, the theory was proven by a Greek scientist, Dr Ionnais Sakkas. Sakkas recreated the invention using historical facts and figures. He set up 70 mirrors held by 70 men and directed them towards a boat that was 160 feet away. Very soon, the boat began to burn.
7. The Odometer
An odometer is a device used to measure distance covered. The word “odometer” comes from the Greek word hodo which means “way” or “road.” Many people confuse the odometer with the speedometer, but they are very different devices. A speedometer measures the speed of a vehicle whereas the odometer measures the distance traveled.
The odometer can now be seen in nearly every vehicle and is an indicator of how far a vehicle has traveled and therefore of its history and usage.
8. Archimedes’ Catapults
When his home city of Syracuse needed Archimedes the most, he was there to help. This ancient inventor discovered many weapons of war that could be used to protect Syracuse from the Romans. One such invention was the catapult or “stone thrower.”
The catapult was a system of propelling heavy stones or objects at enemy ships to destroy them. This kind of machine usually had a bucket in which the projectile was kept, and the missile was fired from the catapult manually.
During the war between Rome and Syracuse, Syracuse managed to hold off the enemy for two years before it was finally defeated.
9. The Law of the Lever
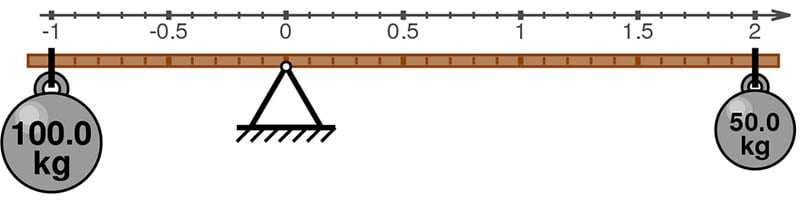
We often see shopkeepers weighing fruit and vegetables in old-fashioned manual scales. These weighing machines work on the principle of equilibrium, which can be achieved using the lever. The lever works on the principle of the center of mass, another example of which is the see-saw.
The lever is basically a rod placed on a triangular beam called a fulcrum which balances the weight. Archimedes’ law states that that:
if the distance a from the fulcrum to where the input force is applied (point A) is greater than the distance b from the fulcrum to where the output force is applied (point B), then the lever amplifies the input force. On the other hand, if the distance a from the fulcrum to the input force is less than the distance b from the fulcrum to the output force, then the lever reduces the input force. (Wikipedia)
10. Discovery of Infinitesimals
Infinitesimals in the ancient Greek period were the equivalent of modern-day calculus. An infinitesimal is a quantity which does not exist but can be made real using limits. Here, we come to the point of limits, continuity, and differentiability.
A function is continuous when its left-hand limit becomes equal to its right-hand limit. The limit is a term that calculates a tiny quantity. Infinitesimal therefore means an extremely or infinitely small quantity.
Archimedes can be said to have introduced calculus through infinitesimals long before Newton and Leibnitz gave us the rules of calculus.
11. Shapes and Their Design
Many years ago, people used to measure time using the stars and the moon, and from that time onwards, people have had to differentiate between different shapes and structures.
At that time people didn’t know about 2D and 3D shapes; they only knew of lines, circles, cubes, spheres, pentagons, etc. That was when Archimedes started thinking of parabolas, eclipses, and hyperbolas. Archimedes introduced the idea of projectile motion with the help of the parabola.
Different equations depict different concepts, and Archimedes showed us that the area of a parabola intersected by a straight line is equal to 0.75 times the area of a triangle inscribed in the parabola and the straight line.
12. The Formula for Surface Area and the Area of a Sphere
A sphere is a 3D circle which comprises of four circles laid together edge to edge. Calculating its surface area as well as its volume was not an easy task. Archimedes was able to calculate the surface area as well as the volume of the sphere by first calculating the surface area of the sphere using 6πr2. The volume is 2πr3.
The creation of these formulae has allowed us to easily calculate the volume and surface area of celestial bodies like the sun, the earth, and the moon.
Conclusion
Archimedes was a person of great importance. As well as being a renowned mathematician, inventor, scientist, and philosopher, he was also a true patriot. Archimedes is an example of the Classical as well as the Hellenistic period of ancient Greece. He died protecting his city Syracuse from the Romans using mathematical calculations and experiments.
Great philosophers lead to greater philosophies, and the inventions of Archimedes have had an enormous impact on our daily lives and made them much easier.
“Give me a place to stand, and I will move the world,” is a famous quote from Archimedes which motivates people and encourages them to pursue their individual talents.
While the ancient Greeks were heavily involved in art and culture, Archimedes was an example of a mathematician and philosopher who also gave the world some of its greatest inventions.